Motivation

R is a programming language used heavily in statistical and data analytic applications. It is open-source software supported by a large community of academics and practitioners who have created numerous libraries to extend its capabilities. Versions of R are available on all major computing platforms (Windows, Mac OS/X, and Linux) and installation is quite simple. If you are using a laboratory computer, likely it will be installed already. R is nice because you can use it simply for data analytics (reading, plotting, and analyzing data) just by knowing a few function calls. But it is also nice because it is a full-fledged programming language. Many tasks that you think would be ideal for MatLab or Mathematica (vector and matrix operations, for example) are also easily accomplished in R. Most introductory tutorials in R focus on the data analytics. This tutorial focuses on R as a programming language.

Organization

The first procedural language I learned was FORTRAN. Ever since then, when I need to learn a new language I try to find out as quickly as possible how to do what I used to be able to do with FORTRAN: assign and display variables, branch on conditional statements, perform a loop of statements repeatedly, and organize code into functions or subroutines. Once I know those essentials, I can slow down, relax, and begin to learn why the new language might be better than FORTRAN. Let’s use that approach with R.

Getting Started

Assign and Display Variables

a=50
a
## [1] 50

The first command assigned the value 50 to the variable ‘a’. The second command caused the value of ‘a’ to be returned to the console for display. The display showed that ‘a’ consists of a single element whose first value (that is what the ‘[1]’ means) is 50.

a/10
## [1] 5
  1. You enter a new assignment command; for example ‘a=3’; Or,
  2. You quit the session or close the program; for example, enter ‘q()’; Or,
  3. You explicitly remove the variable using the command ‘rm(a)’.
rm(a)
a
a = 50
str(a)
##  num 50
a="hello"
str(a)
##  chr "hello"

As you can see, the type of variable a changed from numeric (“num”) to character (“chr”) by assigning the string value “hello” to the variable. Operations that are possible on one type of object may cause errors when used with another type of object. Try this:

a="hello"
str(a)
a/50
a=c(1,2,4,8)
a
## [1] 1 2 4 8
length(a)
## [1] 4

Here we used the function c() to create a vector of four numbers ranging from 1 to 8. [c() stands for ‘concatenate’: it can be used to concatenate multiple short lists into one long list.] We then used the function length() to check how long a vector we had created.

1:50
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
## [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
a=1:50
a
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
## [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
a <- 1:50
a
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
## [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

However, in keeping with R tradition, from now on, we will use = only to assign named arguments in lists (see later) and we will use <- for all other assignments. This is what Google [recommends] (https://google-styleguide.googlecode.com/svn/trunk/Rguide.xml). It requires an extra keystroke to type the back arrow (‘<-‘) but there is a shortcut in RStudio (type <ALT>-). To improve readability, we will try to remember to include some extra spaces around the back arrow as well.

a <- 1:10/5
a
##  [1] 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0

Observe that R took the vector 1:10 and divided each component of the vector by 5. That is important to keep in mind when working with vectors: R will apply operations to each component. You might have expected the answer to be

[1] 1 2

Suppose that is the answer you really wanted. Write down the statements, modified using parentheses (()) to get this as the answer.

Branch on Conditionals

The next major requirement of a programming language is the ability to branch on a condition.

a <- 3
if (a==3)print("It's a three.") else print("It's not a three.")
## [1] "It's a three."

Note that the test for equality is the binary operator “==”. If you had used “=” it would have caused an error.

if (a==3){print("It's a three!");print("It's a three!")} else print("It's not a three.")
## [1] "It's a three!"
## [1] "It's a three!"
if(a==3){
  print("It's a three!")
  print("It's a three!")
  } else {
  print("It's not a three.")
}
## [1] "It's a three!"
## [1] "It's a three!"

Observe that we used the curly braces after the else statement even though there was only one statement to execute in that case. This is considered good coding style.

Perform a Loop of Statements Repeatedly

for (i in 1:5) print(i)
## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

The variable i acts as an iterator, looping through the elements of the vector 1:5.

for (i in 1:5) {b <- 2^i; print(b)}
## [1] 2
## [1] 4
## [1] 8
## [1] 16
## [1] 32

That is, to execute a block of code in a loop, combine the for() statement with a block of code enclosed in curly braces ({}) and separated with semi-colons (;) or carriage returns.

a <- 1:5
b <- 2^a
b
## [1]  2  4  8 16 32

Organize Code into Functions and Subroutines

FORTRAN has the concept of a subroutine which is a block of code that is executed whenever the subroutine is called and a function in which a block of code is executed whenever the function is called and it returns a value computed within the function. In R, a subroutine would simply be a function that does not return a value.

f <- function(x){x^2}
f(3)
## [1] 9
f(18)
## [1] 324

Observe that the variable name f has been assigned a function definition. From now on, f() can be used as a function (until it is assigned something else, or the session ends, or you enter the remove command rm(f)). It can be confusing to think of variables sometimes having values and other times representing functions. So, from now on, we will refer to the letter f as a symbol. You can list the symbols that have been defined in your session using the command ls() and you can get information about what object is stored in the symbol using the command str(). For example, try typing the following:

str(f)
## function (x)  
##  - attr(*, "srcref")= 'srcref' int [1:8] 1 6 1 21 6 21 1 1
##   ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x0000000012b76158>

The result is not helpful to ordinary programmers like me. Here is what is more helpful:

f
## function(x){x^2}
## <bytecode: 0x0000000014a02420>

That is, if you type the symbol, R will display what value it holds.

f <- function(x){result <- 2^x;result}
f(3)
## [1] 8
f <- function(x){result <- 2^x}
f(3)

Observe that, in both cases, the function squares the value of the argument ‘x’ and assigns the result to the symbol ‘result’. However, in the first case, the value is returned from the function by virtue of it being listed (result) as the last statement in the function. In the second case, nothing is returned because the last statement of the function is an assignment statement (result <- x^2). Assignment statements have no return value.

Local-Global Scoping Rules

x <- 4
f <- function(x){x^2}
f(5)
## [1] 25
x
## [1] 4

The symbol x is used twice: once outside the definition of the function (x <- 4) and once inside the function (x^2). When the function is called as f(5), the argument of the function is taken to be (x=5) and the value 25 is returned. However, if we check the value of the symbol x, it still has the value 4. That is, the arguments of the function are treated as local variables within the function. But consider the next example:

rm(a)
f = function(x){x^a}
f(3)

This results in an error object 'a' not found. Try it again as follows:

a <- 2 
f(3)
## [1] 9

In this example, we removed the symbol a from the session (rm(a)) and defined a function which uses two symbols: x and a. The symbol x is the argument of the function but the symbol a is not assigned anywhere inside the function. When we call the function with argument x=3, we get an error because the symbol a cannot be found. We then assign a value to the symbol ‘a’ (‘a <- 2’) and try again. This time it works: we get the value 9=3^2. This shows us that if R cannot find a symbol defined in a function it will search outside the function (i.e. to the session) to find it.

But now consider this example:

f <- function(x){a <- 2;x^a}
a <- 3
f(3)
## [1] 9
a
## [1] 3

In this example, we defined the symbol a both inside and outside the function. It is assigned the value 2 inside the function and the value 3 outside the function. In this case, a acts like a local variable inside the function: it has no effect on the value of a outside the function.

Suppose we really wanted to change the value of a outside the function as part of the function? How would we do it? We can change the value of symbols outside a function by using a stronger version of assignment operator: Use <<- (double-back arrow).

f <- function(x){a <<- 2;x^a}
a <- 3
f(3)
## [1] 9
a
## [1] 2

Here, by using the double-back arrow inside the function, we change the value of the symbol a in the session whenever we call the function f(). This is a dangerous feature! Avoid using it if you can. Use it only if you have complete control over the context in which your program will run.

Function Arguments

f <- function(x){x^2}
f()

This results in an error: 'x' is missing.

Note that R did not complain about the missing argument until it actually tried to use it as part of a calculation. The error occurred when it tried to evaluate x^2. In other languages, you would have received an error sooner. This is called lazy evaluation and can be quite useful.

Suppose we want to allow the user of our function to call it without any arguments? In that case, we simply need to provide a default value for any argument which can be omitted.

f <- function(x=0){x^2}
f()
## [1] 0
f(4)
## [1] 16

Here we have provided a default value for the argument x (x=0). Now it is possible to call the function both with and without an argument and get a reasonable answer in each case. [Also, note that we used the equals sign to set the default (x=0) and not the back-arrow. This is consistent with our convention to use the equals sign in lists (such as argument lists) and the back-arrow everywhere else.]

R is also beautifully flexible when you have multiple arguments in the argument list. Consider this example:

pow <- function(x=0,a=1){x^a}
pow()
## [1] 0
pow(3)
## [1] 3
pow(3,2)
## [1] 9
pow(2,3)
## [1] 8
pow(a=2,x=4)
## [1] 16
pow(a=1000)
## [1] 0

Here, we have defined a function with two named arguments (x and a) and we have assigned default values to each of these two arguments (x=0 and a=1). As a result, look at all the different ways we can call this function and get valid results! We can call it with no arguments (pow()) because both arguments have defaults. We can call it with just the first argument (pow(3)) because the second argument has a default. We can call it with both arguments, but the order is important (pow(3,2) is different from pow(2,3)). But if we know the names of the arguments, then we can call them in any order provided we assign the values by name (pow(a=2,x=4)). We can also call the function with just the arguments we want and accept the defaults for the other arguments (pow(a=1000)).

You will take advantage of this feature as you learn R. For example, you will begin using some library functions in their very simplest form, accepting all of the defaults. Then, as you learn more of the capabilities of the function, you will take more control and assign values to some of the named arguments to get exactly the result you want.

Scripts

To this point, we have demonstrated that R is a fully functioning procedural language, capable of assignment statements, conditional branching, loops, and function definitions. To be really useful as a programming language, however, we have to have a means of saving our code and executing it again at a later time. In R, this is accomplished with scripts. Scripts are simply text files of R statements which can be executed all at once, simply by loading the file.

print("Hello, world!")
source("HelloWorld.R")

This will likely cause an error: No such file or directory.

As you can see, the source command did not work. The reason is that the default R directory did not match the directory in which we saved the file. One way to solve this problem is to be more explicit:

source("C:/Users/pj16/Documents/00pj9/PJ Centric/01 Projects/GDR_Educate/HelloWorld.R")

In your case, you would use the file path matching the directory where you saved the file. Observe that the source() command caused the script to be read and executed (the print statement in the script file was executed). Another way to solve the directory problem is to first set the working directory (setwd()) of the R session. Then you can call the source() command in short form:

setwd("C:/Users/pj16/Documents/00pj9/PJ Centric/01 Projects/GDR_Educate/HelloWorld.R")
source("HelloWorld.R")

[Note to Windows users: you can use File Explorer to get directory paths but they will be in the form “C:16\00pj9Centric\01 Projects_Educate” using backslashes (‘’) instead of forward slashes (‘/’). You must convert them to forward slashes for R or insert a backslash in front of each backslash, as in: “C:\Users\pj16\Documents\00pj9\PJ Centric\01 Projects\GDR_Educate”.]

print("Hello, world!")
## [1] "Hello, world!"
pow <- function(x=0,a=1){x^a}

testpow <- function(){
  print(pow(3,2))
  print(pow(2,3))
}
source("HelloWorld.R")
testpow()
## [1] 9
## [1] 8

You should now begin to see how to organize large projects into scripts containing different functions. Functions in one script can call functions in another script provided only that all the scripts are loaded into the R session using the source() command.

That has the effect of copying the selected text to R console window and executing it.

This is great for debugging. A related trick is to put the cursor on any line in the script file you want to execute and hit the ‘<CTRL. r’ key combination. That line will be executed and the cursor will advance to the next line. So you can execute several lines in sequence by simply hitting ‘<CTRL r’ repeatedly.

Fun with R

So, R is a procedural language that can do everything an old language like FORTRAN can do. What can it do better? In this section, we will explore some of the data visualization possibilities with R. It will also give us some practice with working with vectors, matrices, and loops.

x <- 1:100/10
y <- sin(x)
y
##   [1]  0.09983342  0.19866933  0.29552021  0.38941834  0.47942554  0.56464247
##   [7]  0.64421769  0.71735609  0.78332691  0.84147098  0.89120736  0.93203909
##  [13]  0.96355819  0.98544973  0.99749499  0.99957360  0.99166481  0.97384763
##  [19]  0.94630009  0.90929743  0.86320937  0.80849640  0.74570521  0.67546318
##  [25]  0.59847214  0.51550137  0.42737988  0.33498815  0.23924933  0.14112001
##  [31]  0.04158066 -0.05837414 -0.15774569 -0.25554110 -0.35078323 -0.44252044
##  [37] -0.52983614 -0.61185789 -0.68776616 -0.75680250 -0.81827711 -0.87157577
##  [43] -0.91616594 -0.95160207 -0.97753012 -0.99369100 -0.99992326 -0.99616461
##  [49] -0.98245261 -0.95892427 -0.92581468 -0.88345466 -0.83226744 -0.77276449
##  [55] -0.70554033 -0.63126664 -0.55068554 -0.46460218 -0.37387666 -0.27941550
##  [61] -0.18216250 -0.08308940  0.01681390  0.11654920  0.21511999  0.31154136
##  [67]  0.40484992  0.49411335  0.57843976  0.65698660  0.72896904  0.79366786
##  [73]  0.85043662  0.89870810  0.93799998  0.96791967  0.98816823  0.99854335
##  [79]  0.99894134  0.98935825  0.96988981  0.94073056  0.90217183  0.85459891
##  [85]  0.79848711  0.73439710  0.66296923  0.58491719  0.50102086  0.41211849
##  [91]  0.31909836  0.22288991  0.12445442  0.02477543 -0.07515112 -0.17432678
##  [97] -0.27176063 -0.36647913 -0.45753589 -0.54402111

Observe that y is a vector of length 100. How can you visualize vectors? The plot function is great for visualizing vectors:

plot(y)

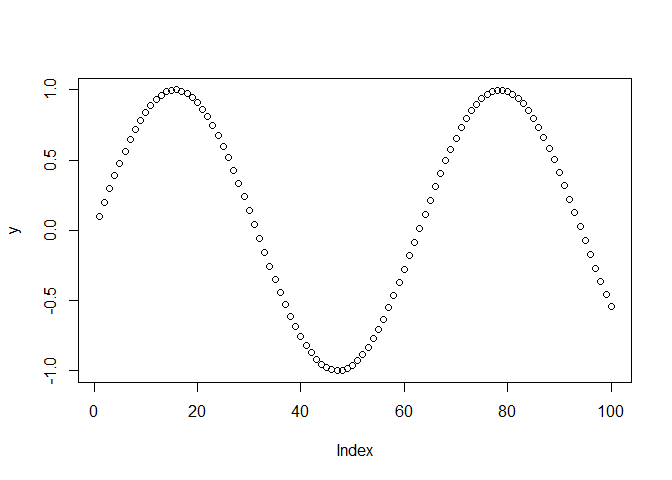
Look for the R Graphics window to see the output of this function.

As you learn more about the defaults for the plot function, you will have greater control over the appearance of your plot. For example, suppose we want to change the color (argument ‘col’) and the title (argument ‘main’) of the plot:

plot(y,col="red",main="The Sine Curve")

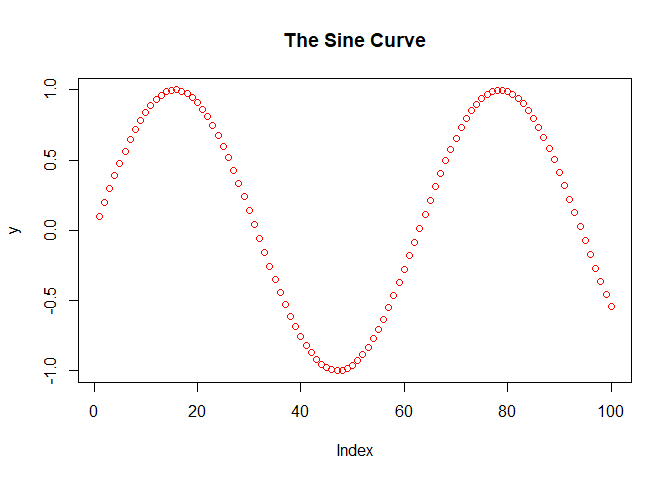
You can learn more about the parameters which control the appearance of the plot at plot

There is a good tutorial on plotting at Intermediate Plotting

a <- -0.966918
b <- 2.879879
c <- .765145
d <- .744728
n <- 100000
x <- .1
y <- .1
xVector = rep(0,n)
yVector = rep(0,n)
for(i in 1:n) {
  newx <- sin(y*b) + c*sin(x*b)
  newy <- sin(x*a) + d*sin(y*a)
  x <- newx
  y <- newy
  xVector[i] <- x
  yVector[i] <- y
}

This creates two vectors, xVector and yVector, each of length 100,000. What is interesting is to plot them together as a scatterplot:

plot(xVector,yVector)

You can improve the appearance of the plot by replacing certain defaults as follows:

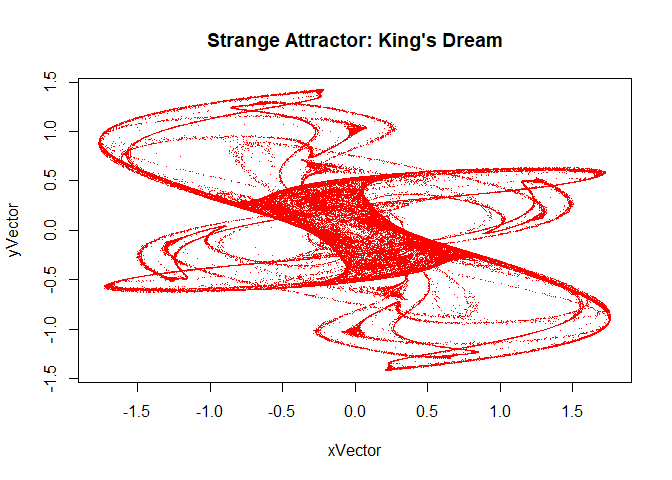
plot(xVector, yVector, pch=".", col="red", main="Strange Attractor: King's Dream")

The named argument ‘pch’ refers to the point character, the style of point used. This code came from [Making Simple Fractals in R] (http://hewner.com/2012/10/09/making-simple-fractals-in-r/)

m <- matrix(1:10,10,10)
m
##       [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [1,]    1    1    1    1    1    1    1    1    1     1
##  [2,]    2    2    2    2    2    2    2    2    2     2
##  [3,]    3    3    3    3    3    3    3    3    3     3
##  [4,]    4    4    4    4    4    4    4    4    4     4
##  [5,]    5    5    5    5    5    5    5    5    5     5
##  [6,]    6    6    6    6    6    6    6    6    6     6
##  [7,]    7    7    7    7    7    7    7    7    7     7
##  [8,]    8    8    8    8    8    8    8    8    8     8
##  [9,]    9    9    9    9    9    9    9    9    9     9
## [10,]   10   10   10   10   10   10   10   10   10    10

What is a good way to visualize a matrix? The image() function displays the matrix as a table of colored boxes, where the colors communicate the values of the matrix entries.

image(m)

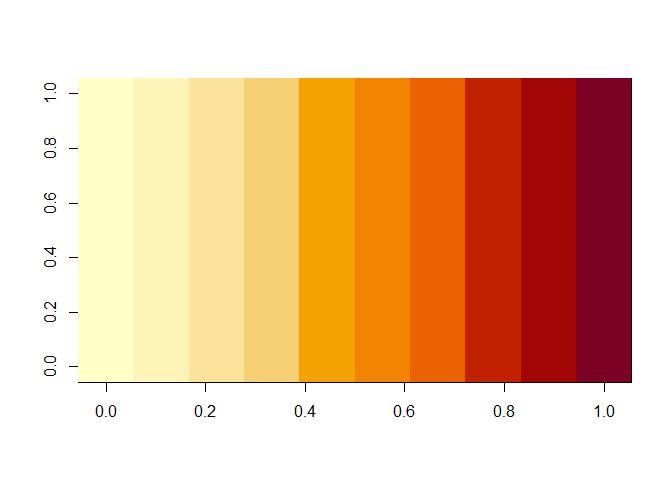
That is not the result I wanted: it has the rows and columns reversed from what I want. So let’s take the transform of the matrix first, using t():

image(t(m))

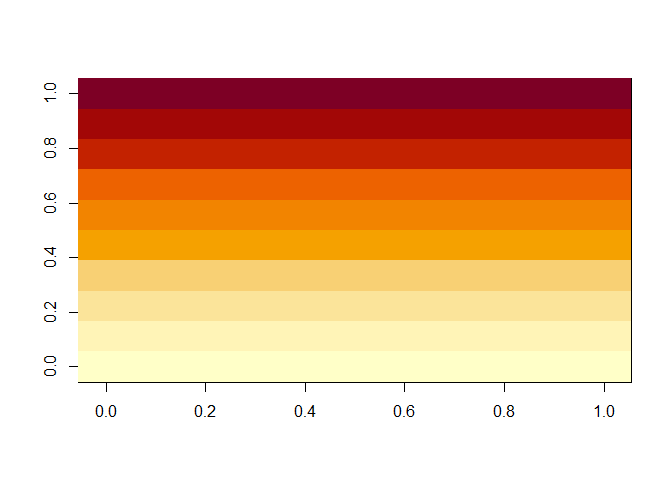
There, that’s better. Now the rows match the vertical dimension and the columns match the horizontal dimension.

volcano

You should see a display of a pre-defined matrix. It consists of the elevation readings across a grid of different latitude and longitudes of the Maunga Whau volcano, the highest of the New Zealand volcanos.

So, to visualize this matrix, simply enter the following:

image(volcano)

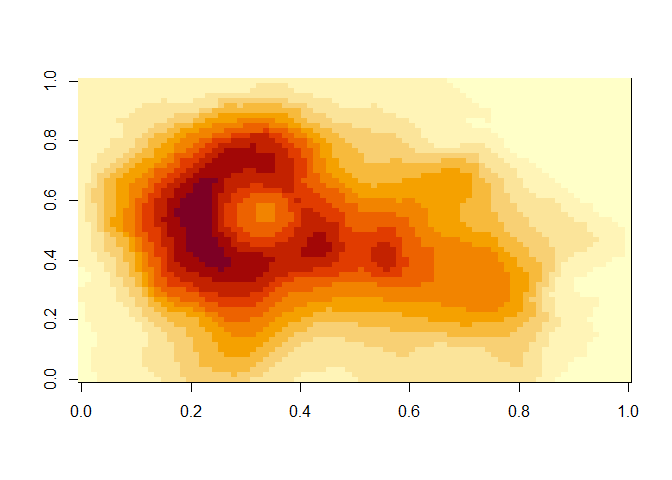
As you can imagine, one of the defaults for this function would be the list of colors to use. We can use a nice color selection function to get a better list:

newcolors <- terrain.colors(100)
image(volcano,col=newcolors)

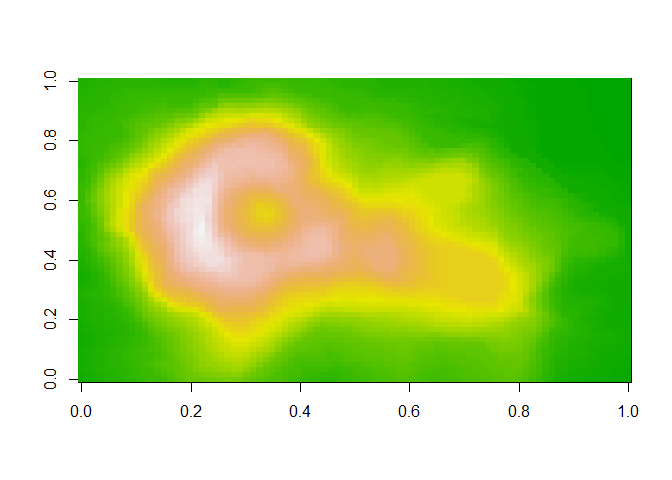
That looks better.

install.packages("plot3D", repos='http://cran.us.r-project.org')
## Installing package into 'C:/Users/pj16/Documents/R/win-library/4.0'
## (as 'lib' is unspecified)
## package 'plot3D' successfully unpacked and MD5 sums checked
## 
## The downloaded binary packages are in
##  C:\Users\pj16\AppData\Local\Temp\Rtmp4gfoYY\downloaded_packages

And

install.packages("rgl",repos='http://cran.us.r-project.org')
## Installing package into 'C:/Users/pj16/Documents/R/win-library/4.0'
## (as 'lib' is unspecified)
## package 'rgl' successfully unpacked and MD5 sums checked
## 
## The downloaded binary packages are in
##  C:\Users\pj16\AppData\Local\Temp\Rtmp4gfoYY\downloaded_packages
library(plot3D)
## Warning: package 'plot3D' was built under R version 4.0.5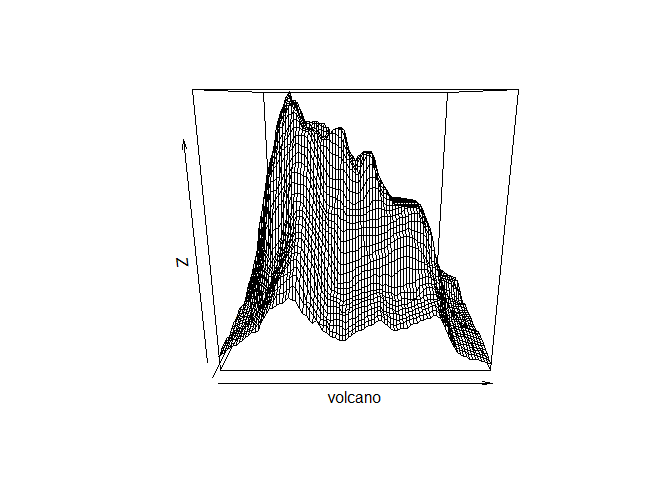
persp(volcano)

That is interesting but we will have to fuss with the parameters (i.e. read the documentation) to get it to look better:

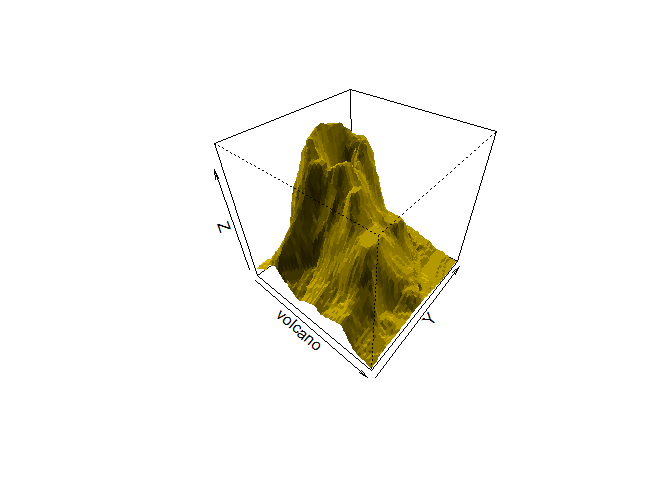
persp(volcano,theta=40,phi=40,col="gold",border=NA,shade=0.5)

This is a really interesting matrix!

library(rgl);
## Warning: package 'rgl' was built under R version 4.0.5
data(volcano);
z<-3*volcano;
x<-10*(1:nrow(z));
y<-10*(1:ncol(z));
zlim<-range(z);
zlen<-zlim[2]-zlim[1]+1;
colorlut<-terrain.colors(zlen,alpha=0);
col<-colorlut[z-zlim[1]+1];
open3d();
## wgl 
##   1
rgl.surface(x,y,z,color=col,alpha=1,back="lines");
#add the contour map in different color
colorlut <- heat.colors(zlen,alpha=1);
col<-colorlut[z-zlim[1]+1];
rgl.surface(x,y,matrix(1,nrow(z),ncol(z)),color=col,back="fill");

This code came from plot 3d topographic map in R.

You should see a window in a separate application that looks like this (use your mouse inside the window to control the view):

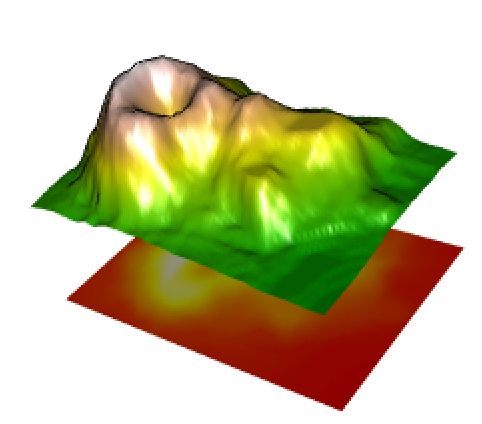
More Fun with R

That is the end of this tutorial. But if you like these plots, try running the following commands (one at a time because they take a long time to plot):

source('http://users.utu.fi/attenka/mandelbrot_set.R')
source('http://users.utu.fi/attenka/julia_set.R')

Visit the following sites to get some interesting code snippets.

Enjoy!